Geography 222 The Power of Maps
...to Geog 222 Main Page and Course Description
...to Geog 222 Syllabus
...to Geog 222 Course Schedule and Lecture Outlines
...to Geog 222 Laboratory Information and Student Projects
Geog 222 Lecture Outline: Map Projections
Update: 10/15/2018
Map Projections
Map projections are an important aspect of all maps, as all maps require the
transformation of the spherical earth to a flat surface


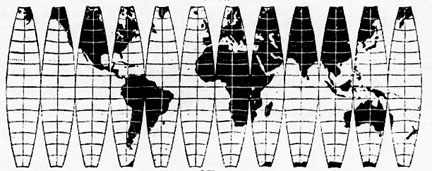
- Flatten out Orange Peel, Springbok, and Toad
PROP) Globe
- on a globe: distance, direction, shape, and areas are not distorted
- Google Earth and other virtual globes
- problems with globes
"Near Globes" and Globe Gores
Map projection process always introduces some kind of distortion
- distortion of area, shape, angles, etc.
- a few have tears and rips in them, but most stretch geography to fill these gaps
- more 'white lies'!
The Power of Maps: maps shape the way we see the world: map projections do this!
Example...
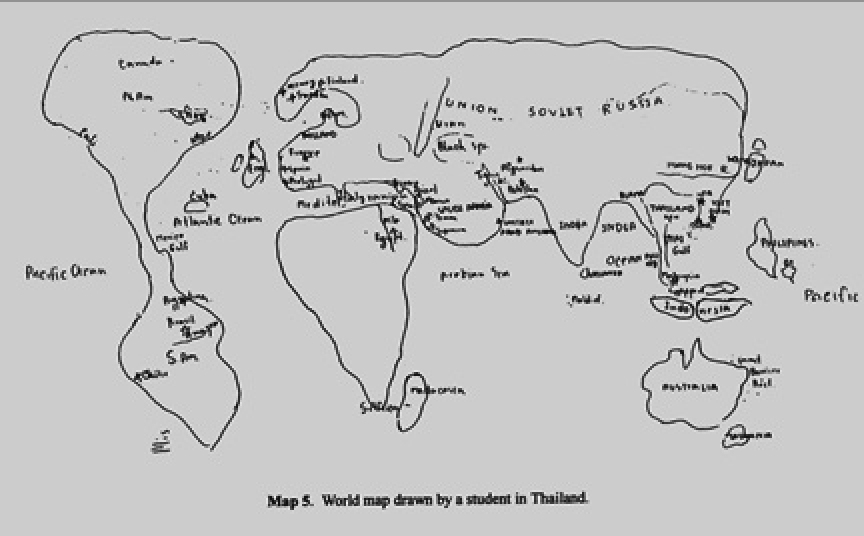
- Children's Mental Maps of World: Looks like the Mercator Projection,
which greatly exaggerates areas in the North.
- From: T. Saarinen. "The Eurocentric Nature of Mental
Maps of the World." Research in Geographic Education 1:2, 1999.
- Kids Mental Maps of World
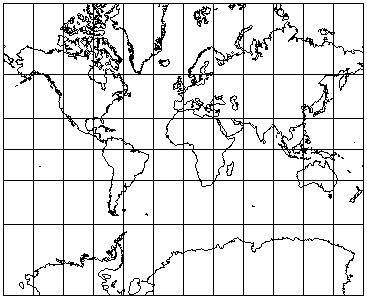
- Mercator Map Projection

- Peters Map Projection
Mercator map projection as good example of how we have become naturalized
(used to) a view of the world that is very distorted and abstract from reality
- it looks normal to us
- but it has greatly modified, stretched, and distorted the earth
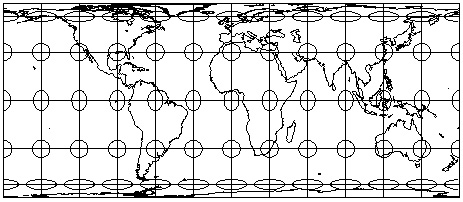
Tissot's Indidicatrix: perfect circles of equal size on the globe; reveal
patterns of distortion on projected maps.
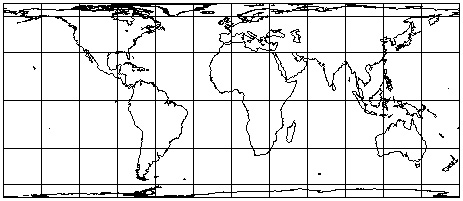
Mercator Projection: Distortion of areas but not shapes...
Equal Area Rectangular Projection (close to Peters): Distortion of shapes but not areas...
Dynamic Map Projections (Mike Rostock) &
with distortion circles added (Ningchuan Xiao)
There are an infinite number of ways to flatten out (project) the earth and
thousands of named map projections
- DEMO) Map Projections in ArcGIS
Cool Free Map Projection Software (Download):
G.Projector
Further understanding of how map projections transform our earth:
Map Projections of other 3D Objects

- Three Dimensional Full Body Scanner
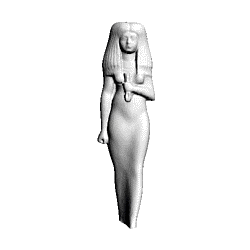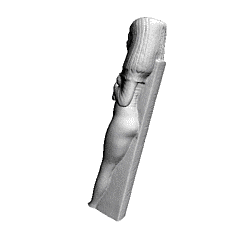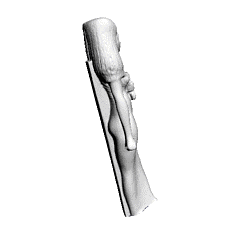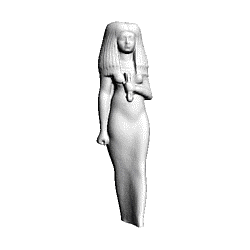

- Isis and Venus Scanned in 3 Dimensions
Scan a human body in 3D in a Full Body Scanner and Flatten using Map Projections:
- Lilla Locurto and Bill Outcault
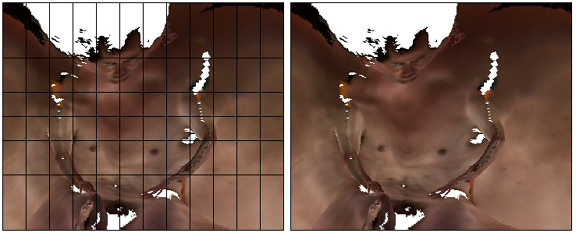
- Mercator Projection of Body
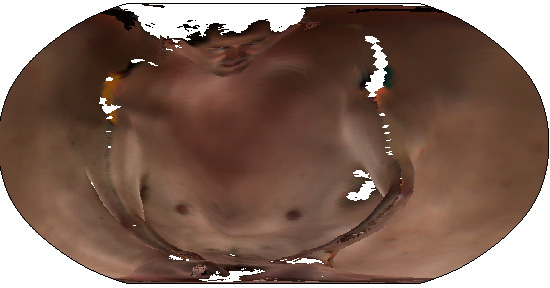
- Robinson Projection of Body

- Amulet Projection of Body
- WWW) Locurto/Outcault
Several issues are of fundamental importance
1. What are the basic characteristics of the map projection process?
- how does map projection work?
2. What kind of flat surface to we project the spherical earth on to?
- flat paper, a cone, and a cylinder
3. How do map projections not distort aspects of our 3D Earth?
- some basic categories of what map projetions preserve.
1. What are the basic characteristics of the map projection process?
- How does map projection work?
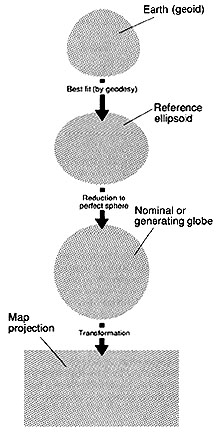
Map projection involves a series of mathematical transformations:
- Earth: geoid
- transformed mathematically to a simpler shape
- Called a reference ellipsoid:
- geodesy
- further transformed (mathematically) into an actual sphere or spheroid
- Called nominal, reference, or generating globe
- further transformed (mathematically) into a flat (plane) surface
- this is where much of the distortion gets added to the map
This is Map Projection: transformation of the spherical surface into a plane surface
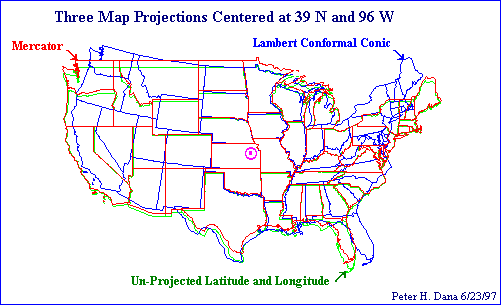
- Three Overlapping Map Projections
(Source)
- all meridians and parallels are transformed in this process: the graticule
- all human and physical earth features (coasts, rivers, lakes, boundaries, etc.) are
also transformed in this process
2. What kind of flat surface to we project the spherical earth on to?
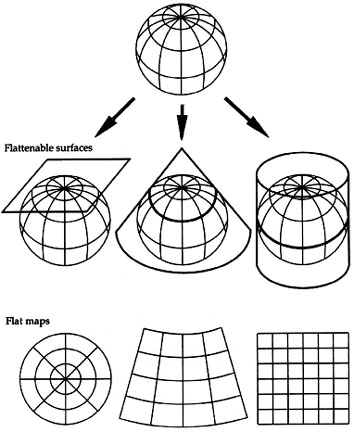
- called "developable surfaces"
PROP) globe and developable surfaces
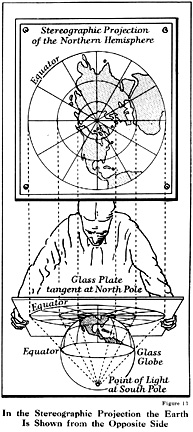
- imagine a light source at the center of the globe
- imagine the lines (continents, boundaries) as they are projected onto the paper
Three basic manipulations of our flat surface
- results in different look and distortions
Developable Surfaces for map projections
- also called projection families
- Projection onto a flat surface: a "plane"
- official name: azimuthal projection families

- Azimuthal Map Projections
(Source)
- Projection onto a cylindrical flattenable surface
- official name: cylindrical projection families

- Cylindrical Map Projections
(Source)
- Projection onto a conical flattenable surface
- official name: conic projection families
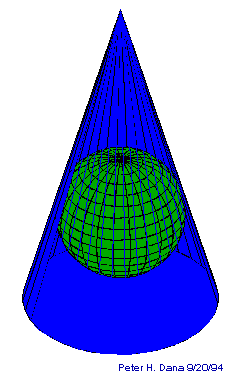
- Conic Map Projections
(Source)
Adjust where the plane, cylinder, or cone touches the globe: Projection Case
- Tangent: touch the globe along one line (or at one point)
- pattern of less and more distortion: where?
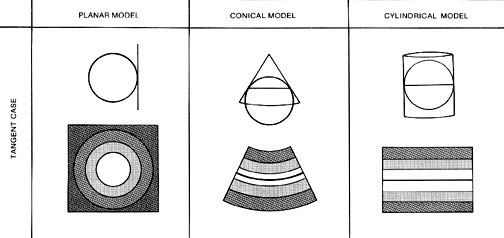
We get different distortions from these different surfaces (projection families)
- Map users and makers should select a map projection with the least distortion
given the phenomena being mapped
- Voyager Map Example: which is best map projection?
- US Census Data Example: which is best map projection?
3. How do map projections not distort aspects of our 3D Earth?
Preservation of areas, shapes, distances, and directions
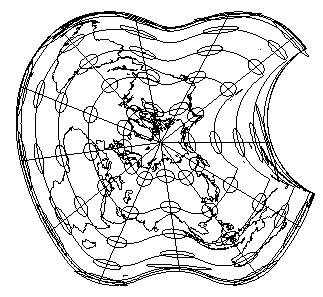
- World projected into apple shape
Again: Tissot's Indicatrix: common way to visualize map projection distortion
Circles on the map: on the globe they are
- all equal in area (size)
- all equal in shape (a circle)
- when projected: see the distortions on the projection
Review five major categories of map projections based on the characteristics they
preserve from the spherical earth
3a. Preserving Area: Equal Area or Equivalent Projections
- Area relationships are preserved
- ArcGIS) GeoCart: Mollweide
- Area representing square mile on map is a square mile everywhere on map
Equal area projections are very important to thematic mapping
- why
- equal area: a good general default for all thematic maps, small or large scale
- best for world map of data in areas: vegetation cover, bedrock types, etc.
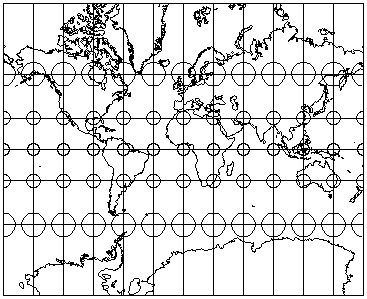
WWW) Peters Projection: Equal Area
WWW) Lambert Azimuthal projection
- if mapping out any data in geographic areas: use equal area projection
- if focused on continent, such as US: use Lambert Azimuthal or Albers Equal Area
- usually 'zoom' in on region or continent
Important: You give up shape (conformality) to preserve area (equivalence)
3b. Preserving Shape: Conformal Projections
Angular relationships are preserved from points
- and shape is preserved for small areas around a given point
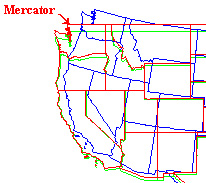
- ex) Four Corners boundary of AZ, NM, CO and UT
- on the globe, these are 90 degree angles
- on a conformal projection, these are 90 degree angles
- alas, areas will be distorted
Important: can never preserve areas (equivalence) and shape (conformality) at the same time
WWW) Mercator map projection is conformal
- Mercator Map Projection
- Mercator: useful for navigation: straight lines on the map are lines of constant compass bearing
(north, south, east, west) in the real world
3c. Preserving Distance: Equidistance Projections
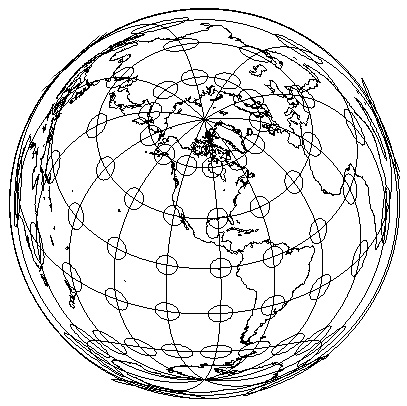
WWW) Azimuthal Equidistant Projection
- centered on one point (Ohio, in this case)
- distance from that point to all other points is correct
- useful for plotting the distance for direct air routes from the point
Important: a map cannot preserve distances and preserve area
3d. Preserving Direction: Azimuthal Projections
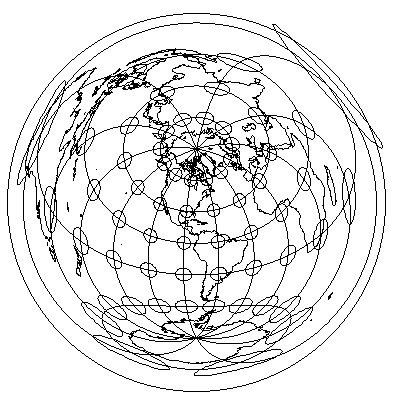
WWW) Orthographic
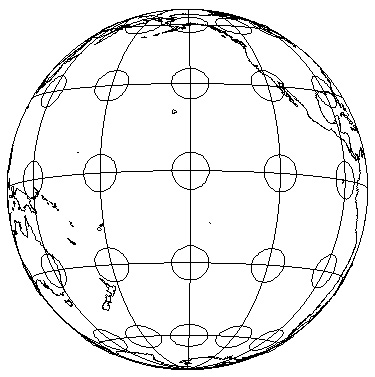
- this example looks like a little globe: orthographic
- such a projection is usually centered on one point (Pacific Ocean, in this case)
- from that point, direction can be correct to all other points
- useful for plotting the direction of some phenomena from a point
- mostly used as inset/locator map
Important: direction can be preserved on equal area (equivalent), conformal (shape preserving), and equidistant
projections
3e. Compromise Projections
WWW) Robinson: National Geographic
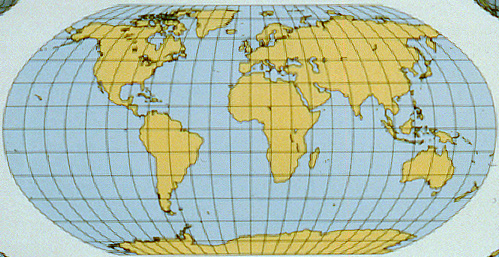
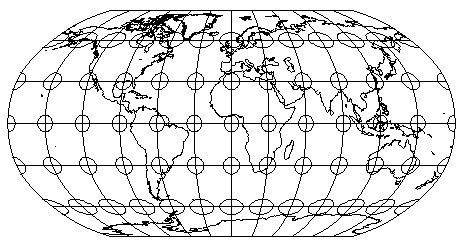
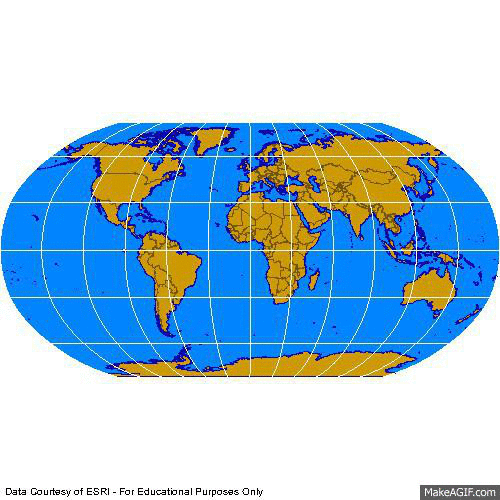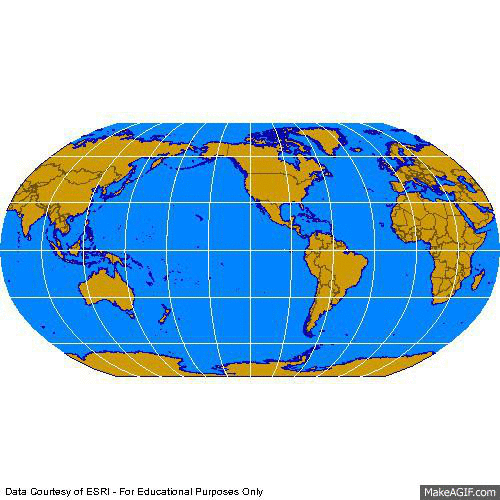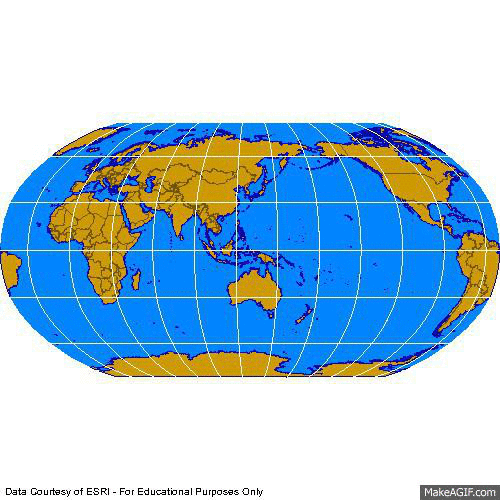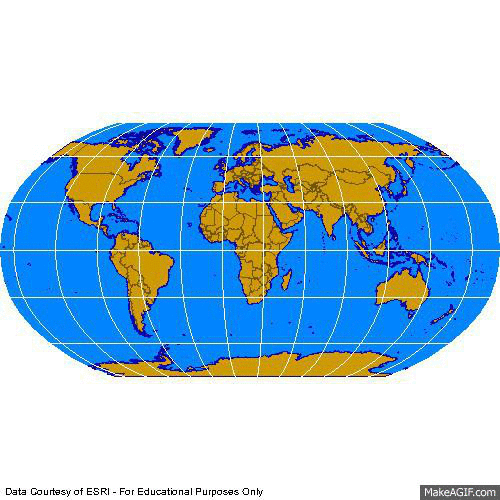
Courtesy of Hayden "Crash" Knisley
A compromise which attempts to preserve enough of area, shape, distance, and direction
so that the earth looks right - but actually preserves none of them.
Summary: Map Projections
1. What are the basic characteristics of the map projection process?
- how does map projection work?
- from the lumpy earth to a sphere to a flat surface
2. What kind of flat surface to we project the spherical earth on to?
- flat surface, a cone, and a cylinder: projection families
- distinctive looks for each
3. What are the basic kinds of map projection distortions?
- some basic categories
- preserving area: equivalent projections
- preserving shape: conformal projections
- cannot preserve both area and shape
- preserving distance: equidistant projections
- cannot preserve both area and distance
- preserving direction: azimuthal projections
- can preserve direction and area OR shape OR distance
- compromise: don't preserve area, shape, distance, or direction
- but minimize distortion of all of these
- good default for world maps
E-mail: jbkrygier@owu.edu
...to Geog 222 Main Page and Course Description
...to krygier teaching page.
...to krygier top page.
OWU Home
OWU Geology and Geography Home